문제
레벨: G5
알고리즘: DP
풀이시간:
힌트 참조 유무:
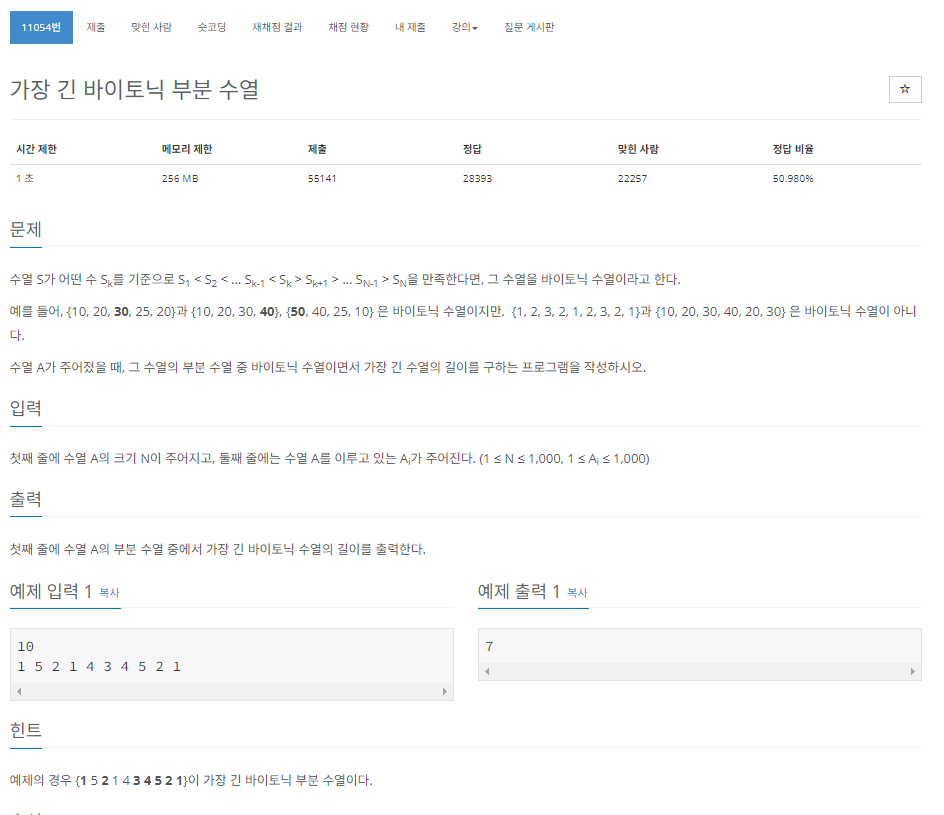
https://www.acmicpc.net/problem/11054
1 번째 시도
위 문제는 LIS와 LDS 합친 문제이다.
참고로 LDS는 LIS를 거꾸로 구현하면 된다.
[1. LIS 구하는 법: O(N^2)]
dp배열에는 LIS 순서가 담긴다.
dp[i]를 구할 때마다 i-1까지 탐색한다.
// N은 배열의 크기
for (int i = 0; i < N; i++) {
// 우선 해당 위치를 본인의 길이(1)로 초기화한다.
dp[i] = 1;
// 현재 원소의 위치에 대하여, 앞의 원소의 값을 비교하며 값을 갱신한다.
for (int j = 0; j < i; j++) {
// 만일 부분 수열이 증가할 가능성이 있다면
if (arr[j] < arr[i]) {
// dp 테이블에 저장된 LIS를 바탕으로 가장 큰 값을 dp[i]의 값으로 갱신한다.
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
// 전체 수열에서 LIS의 값을 갱신한다.
max = Math.max(max, dp[i]);
}[2. LIS 구하는 법: O(NlogN)]
dp배열에는 LIS 원소가 담긴다.
아이디어 컨셉: 숫자마다 간격이 좁을 수록 가장 긴 LIS이다.
원본 배열을 탐색할 때마다 이분 탐색(O(logN))을 해야한다. 그래서 O(NlogN)이다
int len=0;
int idx=0;
for(int i=0; i<n; i++) {
if(arr[i] > memo[len]) {
len +=1;
memo[len] = arr[i];
}else {
idx = binarySearch(0,len, arr[i]);
memo[idx] = arr[i];
}
}
System.out.println(len);
}
static int binarySearch(int left, int right, int key) {
int mid =0;
while(left<right) {
mid = (left+right)/2;
if(memo[mid] < key) {
left = mid+1;
}else {
right = mid;
}
}
return right;
}
정답코드 / Bottom-Up(0번째에서부터 N까지 차곡차곡 구하는 방식)
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
import java.util.StringTokenizer;
public class Main {
static int N;
static int[] seq;
static int[] r_dp;
static int[] l_dp;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
N = Integer.parseInt(br.readLine());
r_dp = new int[N]; // LIS
l_dp = new int[N]; // LDS
seq = new int[N];
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
for (int i = 0; i < N; i++) {
seq[i] = Integer.parseInt(st.nextToken());
}
LIS();
LDS();
int max = 0;
for(int i = 0; i < N; i++) {
if(max < r_dp[i] + l_dp[i]) {
max = r_dp[i] + l_dp[i];
}
}
System.out.println(max - 1);
}
static void LIS() {
for(int i = 0; i < N; i++) {
r_dp[i] = 1;
// 0 ~ i 이전 원소들 탐색
for(int j = 0; j < i; j++) {
// j번째 원소가 i번째 원소보다 작으면서 i번째 dp가 j번째 dp+1 값보다 작은경우
if(seq[j] < seq[i] && r_dp[i] < r_dp[j] + 1) {
r_dp[i] = r_dp[j] + 1; // j번째 원소의 +1 값이 i번째 dp가 된다.
}
}
}
}
static void LDS() {
// 뒤에서부터 시작
for (int i = N - 1; i >= 0; i--) {
l_dp[i] = 1;
// 맨 뒤에서 i 이전 원소들을 탐색
for (int j = N - 1; j > i; j--) {
// i번째 원소가 j번째 원소보다 크면서 i번째 dp가 j번째 dp+1 값보다 작은경우
if (seq[j] < seq[i] && l_dp[i] < l_dp[j] + 1) {
l_dp[i] = l_dp[j] + 1; // j번쨰 원소의 +1이 i번쨰 dp값이 됨
}
}
}
}
}'알고리즘 > DP' 카테고리의 다른 글
| [백준 2225] 합분해 / 자바 / dp ** (1) | 2024.06.10 |
|---|---|
| [백준 2294] 동전2 / 자바 / dp (0) | 2024.06.09 |
| [백준 12865] 평범한 배낭/자바/dp ** (1) | 2024.06.06 |
| [백준 2293] 동전1 / 자바 / dp (1) | 2024.06.05 |
| [프로그래머스 LV3] 연속 펄스 부분 수열의 합 / 자바 / DP (1) | 2024.06.04 |



