문제
레벨: G4
알고리즘: dp ( dp 업데이트 기준 1개 + 일차원 배열)
풀이시간: 1시간
힌트 참조 유무: 유
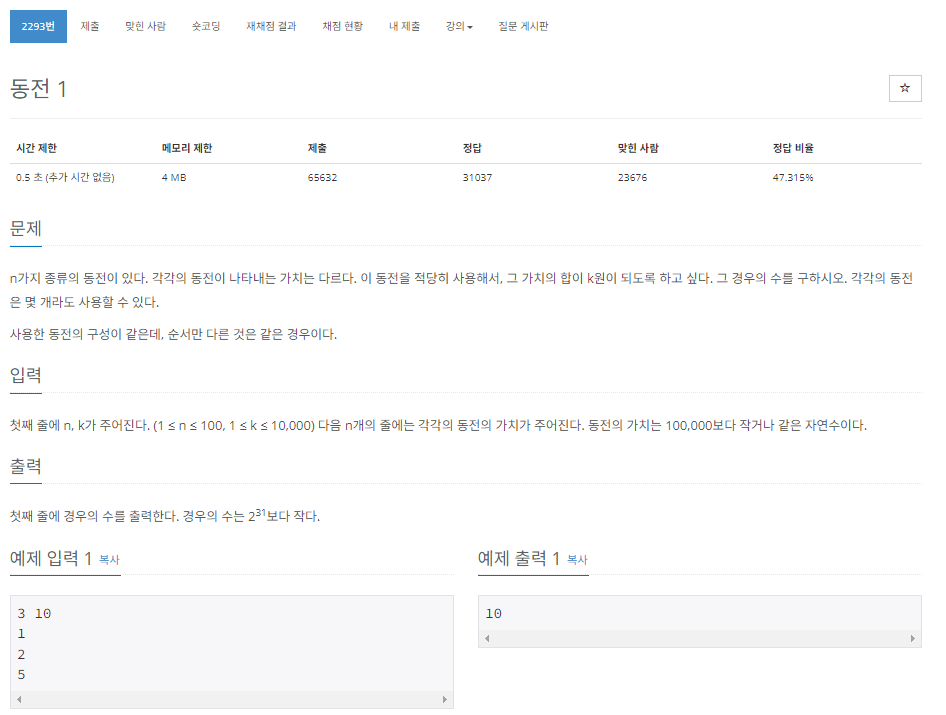
https://www.acmicpc.net/problem/2293
1 번째 시도
[잘못된 알고리즘]
이문제는 dp문제이다. 왜 dp일까?
1원일 때 경우의 수 dp =[1]
2원일 때 경우의 수 = {1,1}(1을 만들 수 있는 경우의 수 x 1을 만들 수 있는 경우의 수) {2,0}(2를 한 번에 만 들 수 있는 경우 수) dp = [1,]
3원일 때 경우의 수 = {3,0} {2,1} dp = [ 1의 경우의수, 2의 경우의 수]
4원일 때 경우의 수 = {4,0} {3,1} {2,2} dp = [ 1의 경우의수, 2의 경우의 수, 3의 경우의 수]
5원일 때 경우의 수 = {5,0} { 4,1} {3,2} dp = [ 1의 경우의수, 2의 경우의 수, 3의 경우의 수, 4의 경우의 수]
.
.
.
.
예를 들어 5원의 경우의 수를 구할 때:
동전 하나로 5를 만들 수 있는 경우의 수 + (dp 배열에 저장되어 있는 4의 경우의 수 * dp배열에 저장되어 있는 경우의 수 1) + (dp배열에 저장되어 있는 3의 경우의 수 * dp 배열에 저장되어 있는 2의 경우의 수) 이다.
그러나 위 풀이는 점화식을 도출하기가 힘들고 중복된 조합을 거를 방법이 너무 복잡하다.
[정답 알고리즘]
(1번) 1원 동전을 썼을 때 dp배열 1에서 10까지 채우기
↓
(2번) 1,2원 동전을 썼을 때 dp배열 1에서 10까지 채우기
↓
(3번) 1,2,5원 동전을 썼을 때 dp배열 1에서 10까지 채우기

dp[i] = dp[i] + dp[i - coin]이다.
1,2원 동전만 썼을 때 K = (1원만 썼을 때의 K가치) + (1,2원 썼을 때 K-2 가치)
- 만약 1,2원 동전만 썼을 때 가치 4원을 도달하고자 한다면 (1원만 썼을 때의 4가치 =1 ) + (1,2원 썼을 때 2 가치 = 2)
- (1,2원 썼을 때 2 가치)는 이전 탐색 때 이미 구해져있다.
(1,2원 썼을 때 2 가치) = (1원만 썼을 때의 2 가치 = 1) + (1,2원 썼을 때 0 가치 = 1) - 1,2원만 썼을 때 가치 4를 구할 때는
1,2원만 썼을 때 가치 2 = { {1,1} {2} }
이배열에 각각 2를 추가해보자 { {1,1,2} {2,2} } 여기에
1원만 썼을 때 가치 4를 더하면 { {1,1,2} {2,2} {1,1,1,1} } 이렇게 총 수가 3이 되는 것이다. - 이 방식이 Bottom-up방식이다.
- DP는 Top - Down 방식과 Bottom-up 방식이 있다.
- 위와 같이 dp 배열을 업데이트해야한다.
나는 한번에 dp배열을 채우려고 했다. 그러나 정답 dp는 동전의 개수에 따라 dp완전순회를 반복했다.
import java.io.*;
import java.util.*;
public class Main {
public static void main(String[] args) throws IOException{
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int K = Integer.parseInt(st.nextToken());
int[] coin = new int[N+1];
int[] cnt = new int[K+1];
cnt[0] = 1;
for(int i = 1; i<=N; i++)
coin[i] = Integer.parseInt(br.readLine());
//coin[] 을 전부 순회하면서 cnt를 더해줌
for(int i = 1; i<=N; i++){
//j는 현재 가질 수 있는 가치의 총량을 의미
for(int j = coin[0]; j<=K; j++){
if(j<coin[i])
continue;
cnt[j] += cnt[j-coin[i]];
}
}
System.out.println(cnt[K]);
}
}
[문제 분류]
dp 업데이트 기준 1개 + 일차원 배열
[DP 다른 방식]

위에 방식은 행을 일차원 배열을 사용했지만 굳이 이차원 배열로 사용하자면 이렇다.
dp[i][j] = dp[i-1][j] + dp[i][j-i]

위에는 동전을 행으로 두고 도달해야할 가치를 열로 두었다. 이 방식을 보여준 이유는 2차원배열로 구현해야할 때 행과 열이 바뀌어도 상관이 없다는 것이다. 자신이 편한 것을 행과 열로 선택하면 된다.
'알고리즘 > DP' 카테고리의 다른 글
| [백준 11054] 가장 긴 바이토닉 부분 수열 / 자바 /dp (1) | 2024.06.08 |
|---|---|
| [백준 12865] 평범한 배낭/자바/dp ** (1) | 2024.06.06 |
| [프로그래머스 LV3] 연속 펄스 부분 수열의 합 / 자바 / DP (1) | 2024.06.04 |
| [백준] LCS/자바 (0) | 2024.05.20 |
| [백준] 내리막길/자바 (0) | 2024.05.13 |



