문제
레벨: LV3
알고리즘: DP(쉬운버전 / cause: 1차원배열 사용)
풀이시간: 1시간
힌트 참조 유무: 유
https://school.programmers.co.kr/learn/courses/30/lessons/161988
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
1 번째 시도
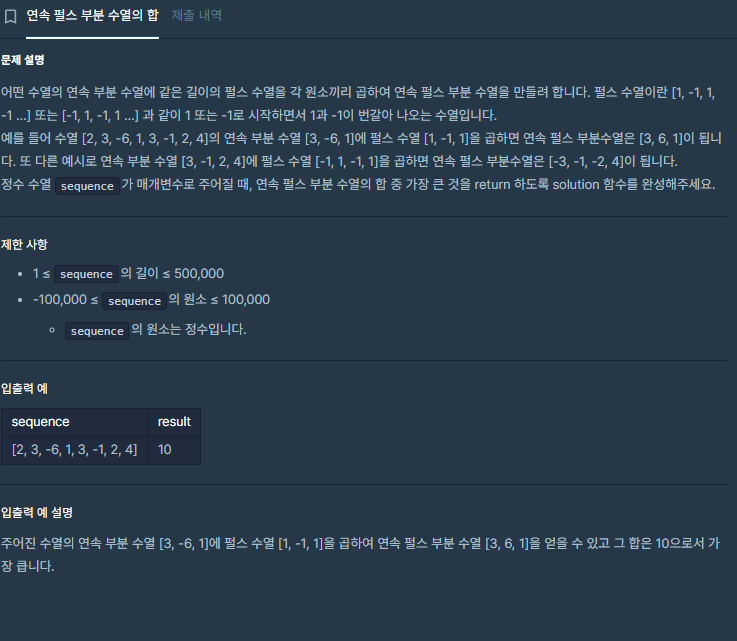
[문제 설명]
(1)
2 3 -6 1 3 -1 2 4 전체 연속배열
x -1 1 -1 1 -1 1 -1 1 펄스배열
-----------------------------
-2 3 6 1 -3 -1 -2 4 = 6 최종합
(2)
2 3 -6 1 3 -1 2 4 전체 연속배열
x 1 -1 1 -1 1 -1 1 -1 펄스배열
-----------------------------
2 -3 -6 -1 3 1 2 -4 = -6 최종합
(3)
-6 1 3 -1 전체 연속배열
x -1 1 -1 1 펄스배열
-----------------------------
6 1 -3 -1 = 3 최종합
(4)
-6 1 3 -1 전체 연속배열
x 1 -1 1 -1 펄스배열
-----------------------------
-6 -1 3 1 = -3 최종합
이처럼 펄스배열의 곱의 합을 구하는 방식은 이렇습니다.
펄스배열 곱의 합 구하는 법 말고도 또 하나 알 수 있을 수 있습니다.
보시는 거와 같이 펄스배열이 1로 시작하든 -1로 시작하던 절대값을 같다는 것입니다.
[아이디어]
그렇다면 맨 처음부터 1로시작하는 펄스배열과 곱한 후 그 중 절대값이 가장 큰 연속된 배열을 찾으면 되지 않을까?
신앙이란 그 순간의 최선의 선택을 한다. 하나님을 믿었으므로
- 연속 펄스 부분 수열의 합
[알고리즘 선택 과정]
연속된 모든 수열을 살펴보아야 하니 브루트 포스가 확실하다. 브루트 포스는 dfs로 구현할 것이다.
입력조건을 보니 dfs로 구현하면 시간초과가 날 것이다. 그럼에도 dfs로 구현해보고 싶었다. dfs가 약해 이 문제는 어떻게 dfs함수를 구현해야 하는지 공부하기 위함이다.
1번
for(int i = 0; i < N; i++) {
if(visited[i] == true)
continue;
visited[i] = true;
dfs(sequence, sum + sequence[i]);
visited[i] = false;
dfs(sequence, sum + sequence[i]);
}2번
public void dfs(boolean seq, int sum) {
if(seq == false) {
ans = Math.max(ans, sum);
return;
}
dfs(false); //배열이 끊긴 경우
dfs(true); //아직 배열을 시작 안 한 경우
dfs(true,) //배열이 계속되는 경우
}둘 다 아니다. 연속된 배열을 dfs로 어떻게 골라서 탐색하지? ==> 불가능
이건 dfs보다는 아래처럼 구현하는 게 나을듯
for(int i = 0 ; i< N; i++) {
temp = 0;
for(int j =i; j <N; j++) {
temp += arr[j];
ans = Math.max(ans, temp)
}
}
[뻘짓으로 인한 얻은점]
완전탐색 = dfs로 생각한 아주 잘못된 나의 잘못된 생각이 이번 기회를 통해 바로잡혔다!
[정답 알고리즘]
- 정답 알고리즘은 dp다.
1. [1, -1, 1, -1...]을 순서대로 곱하는 부분 수열의 합을 기록하기(purse1)
2. [-1, 1, -1, 1 ...]을 순서대로 곱하는 부분 수열의 합을 기록하기(purse2)
3. sequence를 완전 탐색 하면서 값에 펄스 부분 수열을 곱하여 purse1, purse2에 더해주기
4. purse1이나 purse2가 0보다 작아지면 0으로 만들어 주기(0보다 작을 수 없기 때문에)
5. purse1이나 purse2가 answer보다 커지면 answer 변경해 주기
class Solution {
public long solution(int[] sequence) {
long maxSum = 0;
boolean isPositive = true;
long sum1 = 0;
long sum2 = 0;
for (int num : sequence) {
sum1 += isPositive ? num : -num;
sum2 += isPositive ? -num : num;
sum1 = Math.max(0, sum1);
sum2 = Math.max(0, sum2);
maxSum = Math.max(maxSum, Math.max(sum1, sum2));
isPositive = !isPositive;
}
return maxSum;
}
}
'알고리즘 > DP' 카테고리의 다른 글
| [백준 11054] 가장 긴 바이토닉 부분 수열 / 자바 /dp (1) | 2024.06.08 |
|---|---|
| [백준 12865] 평범한 배낭/자바/dp ** (1) | 2024.06.06 |
| [백준 2293] 동전1 / 자바 / dp (1) | 2024.06.05 |
| [백준] LCS/자바 (0) | 2024.05.20 |
| [백준] 내리막길/자바 (0) | 2024.05.13 |



