문제
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명

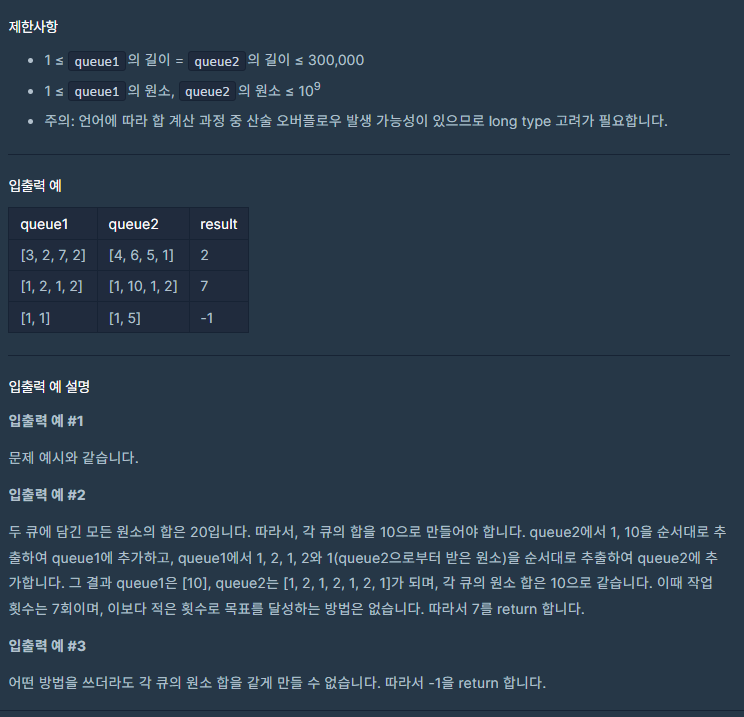
요구사항 정리
- 각 큐의 합이 같도록 하는 최소 횟수
- 넣고 빼는데 '큐라는' 자료구조 특성을 반영해야 함
- 각 큐의 원소 합을 같게 만들지 못한다면 -1을 리턴
해결법
- 두 개를 1/2 씩 맞춘다는 관점보다 하나를 1/2 맞추면 다른 하나는 1/2가 맞춰진다로 생각
- 먼저 두 큐 원소의 합을 저장하는 변수 생성
- 최소 횟수이려면 큐 앞단에 위치한 요소들을 움직여야 함
- A큐의 원소 하나를 빼서 B큐에 넣으면 B큐의 원소 하나도 A큐로 가야함(길이를 맞춰야 하기 때문에)
- A큐 < - > B큐의 원소가 모두 바뀌었을 때도 1/2를 못 맞춘다면 방법이 없으므로 -1 리턴
- 한 큐의 원소를 한 번만 탐색하면 되므로 O(n)
1 번째 코드
class Solution {
public int solution(int[] queue1, int[] queue2) {
long queue1Sum = 0;
long queue2Sum = 0;
long allSum =0;
int result = -1;
for(int i =0; i < queue1.length; i++) {
queue1Sum += queue1[i];
queue2Sum += queue2[i];
}
allSum += queue1Sum + queue2Sum;
//큐1이랑 큐2 원소 바꿨을 때 큐1의 합이 1/2인지 확인
for(int i= 0; i < queue1.length; i++) {
queue1Sum -= queue1[i];
queue1Sum += queue2[i] ;
if(queue1Sum == allSum/2){
result = i;
break;
}
}
return result;
}
}

문제
테스트 하나를 통과했지만 두 개를 통과하지 못했다.
즉, 예외상황을 놓쳤거나 로직이 틀렸다는 것이다.
테스트1 실행결과에서 알 수 있는 것
for 문으로 큐1을 순회할 때 그에 해당하는 인덱스 i를 result로 주입했다.
큐1의 원소가 하나 빠진다는 건 큐2의 원소도 하나가 빠진다는 것이기 때문에 i*2가 result이다.
테스트2 실행결과에서 알 수 있는 것
정답이 7로 홀수이다. 문제를 잘못이해했다. 최종 큐1과 큐2의 길이가 같아야 하는줄 알았다.
그럼, 테스트1 실행결과에서 알 수 있는 것도 소용이 없게된다. 해결법을 수정하겠다.
해결법
- 두 개를 1/2 씩 맞춘다는 관점보다 하나를 1/2 맞추면 다른 하나는 1/2가 맞춰진다로 생각
- 먼저 두 큐 원소의 합을 저장하는 변수 생성
- 최소 횟수이려면 큐 앞단에 위치한 요소들을 움직여야 함
A큐의 원소 하나를 빼서 B큐에 넣으면 B큐의 원소 하나도 A큐로 가야함(길이를 맞춰야 하기 때문에)A큐 < - > B큐의 원소가 모두 바뀌었을 때도 1/2를 못 맞춘다면 방법이 없으므로 -1 리턴- 한 큐의 원소를 한 번만 탐색하면 되므로 O(n)
+
- 큐1이 1/2보다 얼마나 부족한지 넘치는지 계산한다.
- 큐1이 1/2보다 부족하다면 큐2에서 빼온다
- 또 부족하면 큐2에서 또 뻬온다 넘친다면 넘겨준다
ex)
[1,2,1,2] [ 1,10,1,2] - 0번째
[1,2,1,2,1,] [10,1,2] 7 13 -1번째
[1,2,1,2,1,10] [1,2] 17 3 - 2번째
[2,1,2,1,10] [1,2,1] 16 4 - 3번째
[1,2,1,10] [1,2,1,2] 14 6 - 4번째
[2,1,10] [1,2,1,2,1] 13 7 - 5번째
[1,10] [1,2,1,2,1,2] 11 9 - 6번째
[10] [1,2,1,2,1,2,1] 10 10 - 7번째
- 큐1이 원소를 가지는 경우의 수(현재 상태 제외)는 어떻게 될까?
- {1,2,3,} {4}
- {1,2,3,4} {}
- {2,3,4} {1}
- {3,4} {1,2}
- {4} {1,2,3}
- {} {1,2,3,4}
- 큐2의 원소 수 + (큐1의 원소수 -1) 만큼 만 탐색해보고 없으면 -1를 리턴하면 되겠다
2 번째 시도
import java.util.*;
import java.util.stream.*;
class Solution {
public int solution(int[] queue1, int[] queue2) {
long queue1Sum = 0;
long queue2Sum = 0;
long allSum =0;
long halfSum = 0;
int result = 0;
List<Integer> q1 = Arrays.stream(queue1).boxed().collect(Collectors.toList());
List<Integer> q2 = Arrays.stream(queue2).boxed().collect(Collectors.toList());
for(int i =0; i < q1.size(); i++) {
queue1Sum += q1.get(i);
queue2Sum += q2.get(i);
}
allSum += queue1Sum + queue2Sum;
halfSum = allSum/2;
//큐1이 1/2 인지 확인
int queue1Index = 0 ;
int queue2Index = 0 ;
int i =0;
do{
if(queue1Sum > halfSum) {
queue1Sum -= q1.get(0);
q2.add(q1.get(0));
q1.remove(0);
}
else if(queue1Sum < halfSum ) {
queue1Sum += q2.get(0);
q1.add(q2.get(0));
q2.remove(0);
}
i++;
result++;
if(i > (q1.size() + q2.size() -1)){
result = -1;
break;
}
}while(queue1Sum != halfSum);
return result;
}
}
문제점
효율성 문제: List에서 요소를 제거하거나 추가할 때의 시간 복잡도는 리스트의 구현에 따라 다를 수 있지만, 일반적으로 ArrayList를 사용할 경우 요소를 제거하거나 추가하는 데 O(n)의 시간이 소요됩니다. 이는 리스트의 크기가 커질수록 성능 문제를 일으킬 수 있습니다. 특히, 요소를 리스트의 시작 부분에서 추가하거나 제거할 때 나머지 모든 요소들을 이동해야 하기 때문에 비효율적입니다.
해결법
- 자료구조 변경: ArrayList -> Queue로 변경(LinkedList로 구현, 수정 삭제에 좋음)
or
- 알고리즘 변경: 그리드 -> 슬라이딩 원도우
- 두 큐의 요소를 하나의 순환 큐로 간주하고, 요소의 이동 없이 요소의 합만을 계산하여 목표 합에 도달할 수 있는지 확인할 수 있습니다
- ex) {1,2} {3,4} 두 개의 큐가 있다면 {1,2,3,4} 큐 하나로 보기
3번째 시도(그리드)
import java.util.*;
class Solution {
public long getsum(int[] q) {
long sum = 0;
for(int i = 0; i < q.length; i++)
{
sum += (long) q[i];
}
return sum;
}
public int solution(int[] queue1, int[] queue2) {
int answer = 0;
long sum1 = getsum(queue1);
long sum2 = getsum(queue2);
Queue<Integer> q1 = new LinkedList<>();
Queue<Integer> q2 = new LinkedList<>();
for(int i = 0; i < queue1.length; i++) {
q1.add(queue1[i]);
q2.add(queue2[i]);
}
while(sum1 != sum2) {
if(answer > (queue1.length + queue2.length) * 2)
return -1;
int val = 0;
if(sum1 < sum2) {
val = q2.poll();
q1.add(val);
sum1 += (long) val;
sum2 -= (long) val;
}
else if(sum1 > sum2) {
val = q1.poll();
q2.add(val);
sum1 -= (long) val;
sum2 += (long) val;
}
else
{
return answer;
}
answer++;
}
return answer;
}
}
2 번째 코드와 자료구조만 바뀐 것이므로 설명은 생략하겠습니다
3 번째 시도(슬라이딩 윈도우)
import java.util.*;
class Solution {
public int solution(int[] queue1, int[] queue2) {
int n = queue1.length;
int[] a = new int[2*n];
for(int i = 0; i < n; i++){
a[i] = queue1[i];
a[n+i] = queue2[i];
} //새로운 배열 초기화
long target = 0;
for(int i = 0; i < 2*n; i++)
target += a[i];
if(target % 2 != 0) return -1;
target /= 2; // 합이 target이 되는 구간을 찾아야 함
int ans = 0x7f7f7f7f; // 일단 매우 큰 값을 넣어놓고 시작
int en = 0;
long tot = a[0]; // 현재 보는 구간의 합 = a[st]+...+a[en], 범위가 양 끝을 포함(inclusive)한다는 점과 en < st일 땐 a[st]+...+a[2*n-1]+a[0]+...+a[en]을 나타냄에 주의
for(int st = 0; st < 2*n; st++){
while(tot < target){
en = (en + 1) % (2*n);
tot += a[en];
}
// while문을 탈출하면 a[st]+...+a[en] 구간의 합이 target 이상임을 의미
if(tot == target){ // 구간의 합이 정확히 target과 일치할 경우
int moves; // 작업 횟수
if(en < n-1) moves = 3*n + 1 + st + en; // 3n+1번의 연산을 통해 큐1에 첫 번째 원소만 남길 수 있고, 이후 st+en 번의 추가적인 연산을 거쳐 a[st] .. a[en]을 큐1에 둘 수 있음
else moves = st + (en - n + 1);
ans = Math.min(ans, moves);
}
tot -= a[st];
}
if(ans == 0x7f7f7f7f) ans = -1;
return ans;
}
}1단계: 두 개의 대기열을 하나의 배열로 결합
두 개의 대기열이 있다고 가정
- queue1 = [3, 2, 7, 2]
- queue2 = [4, 6, 5, 1]
이를 하나의 배열로 결합하고 쉽게 처리할 수 있도록 원형 배열로 처리합니다.
- a = [3, 2, 7, 2, 4, 6, 5, 1]
이 배열 'a'는 두 대기열을 연속적으로 나타냅니다.
2단계: 목표 합계 계산
a에 있는 모든 요소의 총합을 계산하고 2로 나누어 각 대기열이 이상적으로 도달해야 하는 목표 합을 찾습니다.
- 총합 = 30
- 목표 합계 = 15
3단계: 슬라이딩 윈도우 검색
슬라이딩 윈도우 접근 방식을 사용하여 이 원형 배열 내에서 합계가 목표 합계와 동일한 연속 세그먼트를 찾습니다. 첫 번째 요소에서 시작하도록 창을 초기화합니다.
- st = 0과 en = 0으로 시작하고 첫 번째 요소의 총합 tot = a[0].
슬라이딩 윈도우 시각화
이 창을 a 배열 위로 이동하는 것을 시각화해 보겠습니다.
- 처음에는 창에 첫 번째 요소 [3]만 포함됩니다. 총계(tot)가 목표보다 작으므로 창을 확장합니다.
- 총계(tot)가 목표와 같거나 초과할 때까지 더 많은 요소를 포함하도록 창을 확장하세요. 예를 들어 창이 확장되어 [3, 2, 7, 2]를 포함하는 경우 총계는 이제 14로 여전히 목표보다 낮습니다. 계속 확장합니다..
- 창에 '[3, 2, 7, 2, 4]'가 포함되면 총계는 '18'로 목표를 초과합니다. 이제 처음부터 창을 축소하여 대상에 더 가까워지려고 합니다.
- 대상과 정확히 일치하는 창(예: [7, 2, 4, 2])을 찾으면 원래 대기열에서 이 배열을 달성하는 데 필요한 작업을 계산합니다.
4단계: 동작 계산 및 답변 업데이트
목표 합계와 일치하는 모든 창에 대해 필요한 최소 이동 횟수를 계산합니다.
- 창이 [7, 2, 4, 2](단지 예)인 경우 원래 대기열에서 시작하여 이 배열을 가져오는 데 필요한 이동 횟수를 결정합니다. 여기에는 한 큐에서 요소를 꺼내서 다른 큐에 추가하는 작업이 포함됩니다.
마지막 단계: 최소 이동 횟수 반환
가능한 모든 창을 조사한 후 균형 잡힌 대기열을 달성하는 데 필요한 최소 이동 수를 반환합니다. 그러한 배열이 가능하지 않은 경우(즉, 어떤 세그먼트에서도 목표 합계를 달성할 수 없는 경우) -1을 반환합니다.
이 접근 방식은 총 합계 계산, 원형 배열 조작 및 슬라이딩 윈도우 기술의 조합을 활용하여 최소한의 작업으로 두 대기열의 균형을 맞추는 가능한 모든 방법을 체계적으로 탐색하여 솔루션을 효율적으로 찾습니다.
얻은 점
- Queue자료구조 깊이 공부
- List 구현체 학습
- ArrayList < - > array 변환법 공부
- ArraysList<> = Arrays.asList(int[]) 이거 안됨
- Stream.boxed().collect(Collector.toList())로 List 변환 / ArrayList로 변환 안됨
- 슬라이딩 윈도우/투포인터 알고리즘 지식 획득
- 알고리즘 문제 풀 때 제한사항 확인하여 시간복잡도 상한선 정하기
'알고리즘' 카테고리의 다른 글
| 항하99 TIL 3일차(바탕화면 정리/프로그래머스) (0) | 2024.03.28 |
|---|---|
| 99클럽 코테 스터디 2일차 TIL(최댓값과 최솟값 /프로그래머스) (0) | 2024.03.27 |
| [백준] 7785번 회사에 있는 사람 (0) | 2024.03.25 |
| [프로그래머스] 과제 진행 / 우선순위 (0) | 2024.03.14 |
| [프로그래머스] Lv2 두 원 사이의 정수 쌍 (5) | 2024.03.12 |



