Notice
Recent Posts
Recent Comments
Link
아무튼, 쓰기
[백준 28707] 배열 정렬 / 자바 / 다익스트라 알고리즘 본문
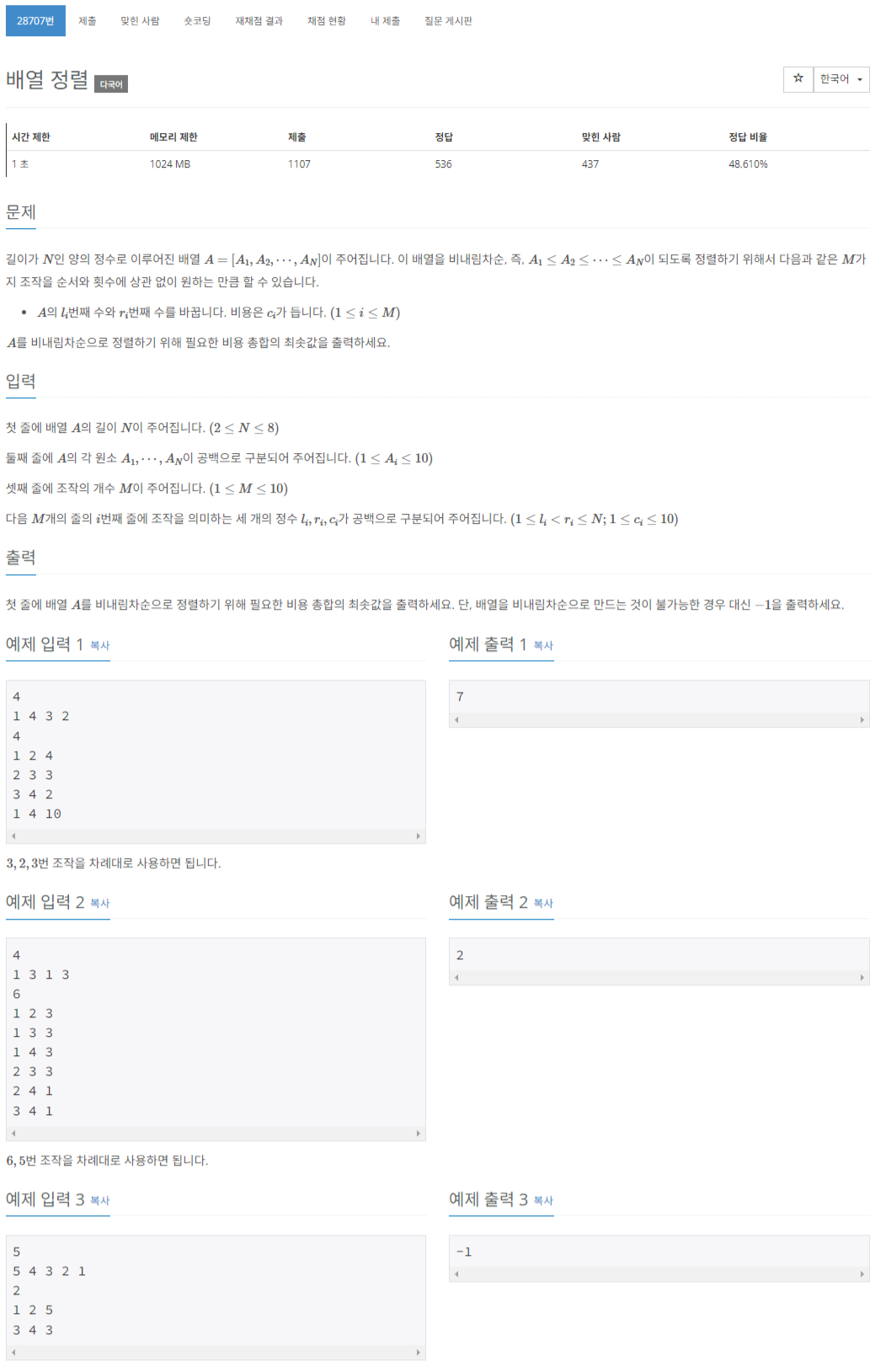
#문제
레벨: G1
알고리즘: 다익스트라 알고리즘
풀이시간: 1시간
힌트 참조 유무: 유
https://www.acmicpc.net/problem/28707
#문제 풀이
이 문제는 다익스트라 알고리즘을 사용한다. 통상적인 다익스트라 알고리즘은 노드에 도입하여 이 문제에 대해서 어떻게 다익스트라 알고리즘을 이용할지 가늠이 안 갈 수도있다.
다익스트라 알고리즘을 적용할 때 노드가 아니라 상태A -> 상태 B로 갈 때 최소 비용이라고 생각하면 이해하기 편할 거다. 만약 예제2번을 들어 설명하자면,
1313 - > 1133 로 갈 때의 최소비용을 저장하는 것이다.
다익스트라 알고리즘을 사용할 수 있는데 또 다른 이유가 있다. 당연한 이야기지만, 우리는 정렬된 정답 배열을 알고있다. 만약 1313이 시작이라면 1133이 정답 배열일테고 1432라면 1234가 정답 배열이다.
우린 1432라는 노드에서 1234라는 노드까지의 최소 비용을 구하면 되는 것이다.
[HashMap 사용]
일반적인 다익스트라 알고리즘은 노드문제여서 노드번호에 따른 배열에 최소 비용을 저장해뒀으면 됐지만, 우린 숫자에 상태이다. 1313 , 1133,1331.... 등 이 상태를 배열에 어떻게 저장해야 할까? 우린 HashMap을 사용해 상태(Key) 비용(Value)를 저장할 것이다.
[십진법으로 숫자 표현]
여러 숫자를 배열그대로 사용한다면 숫자비교 혹은 저장하기 힘들 것이다. 그래서 우린 숫자배열을 하나의 숫자, 즉 십진법을 이용해 사용할 것이다.
#풀이 코드
import java.util.*;
import java.io.*;
public class Main {
// 명령어(상태 변환)를 나타내는 클래스
static class Command implements Comparable<Command> {
int state, cost; // state: 배열의 현재 상태, cost: 현재까지의 비용
public Command(int state, int cost) {
this.state = state;
this.cost = cost;
}
// 비용 기준으로 정렬하기 위한 compareTo 메서드
@Override
public int compareTo(Command o) {
return this.cost - o.cost;
}
}
static int N, M; // N: 배열의 크기, M: 가능한 연산의 수
static int[] A; // 초기 배열
static List<int[]> operations; // 가능한 연산들의 리스트
static final int INF = 1_000_000_000; // 무한대 값 (도달 불가능한 경우를 위함)
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 입력 처리
N = Integer.parseInt(br.readLine());
A = new int[N];
String[] input = br.readLine().split(" ");
for (int i = 0; i < N; i++) {
A[i] = Integer.parseInt(input[i]) - 1; // 0-based 인덱스로 변환
}
M = Integer.parseInt(br.readLine());
operations = new ArrayList<>();
for (int i = 0; i < M; i++) {
input = br.readLine().split(" ");
int l = Integer.parseInt(input[0]) - 1;
int r = Integer.parseInt(input[1]) - 1;
int c = Integer.parseInt(input[2]);
operations.add(new int[]{l, r, c});
}
// 문제 해결 및 결과 출력
int result = solve();
bw.write(result == INF ? "-1\n" : result + "\n");
bw.flush();
bw.close();
br.close();
}
// 다익스트라 알고리즘을 이용한 문제 해결
static int solve() {
int start = encodeState(A); // 시작 상태
int[] sortedA = Arrays.copyOf(A, N);
Arrays.sort(sortedA);
int end = encodeState(sortedA); // 목표 상태 (정렬된 상태)
PriorityQueue<Command> pq = new PriorityQueue<>(); // 우선순위 큐
Map<Integer, Integer> dist = new HashMap<>(); // 각 상태까지의 최소 비용
pq.offer(new Command(start, 0));
dist.put(start, 0);
while (!pq.isEmpty()) {
Command current = pq.poll();
// 목표 상태에 도달한 경우
if (current.state == end) {
return current.cost;
}
// 이미 더 적은 비용으로 해당 상태에 도달한 경우 스킵
if (dist.get(current.state) < current.cost) continue;
// 모든 가능한 연산에 대해 새로운 상태 탐색
for (int[] op : operations) {
int newState = applyOperation(current.state, op[0], op[1]);
int newCost = current.cost + op[2];
// 새로운 상태가 처음이거나 기존보다 적은 비용으로 도달 가능한 경우
if (!dist.containsKey(newState) || newCost < dist.get(newState)) {
dist.put(newState, newCost);
pq.offer(new Command(newState, newCost));
}
}
}
return INF; // 목표 상태에 도달할 수 없는 경우
}
// 배열 상태를 정수로 인코딩
static int encodeState(int[] state) {
int encoded = 0;
for (int i = 0; i < N; i++) {
encoded = encoded * 10 + state[i];
}
return encoded;
}
// 주어진 연산을 상태에 적용
static int applyOperation(int state, int l, int r) {
int[] decodedState = new int[N];
// 상태를 배열로 디코딩
for (int i = N - 1; i >= 0; i--) {
decodedState[i] = state % 10;
state /= 10;
}
// l과 r 위치의 원소 교환
int temp = decodedState[l];
decodedState[l] = decodedState[r];
decodedState[r] = temp;
// 변경된 상태를 다시 인코딩하여 반환
return encodeState(decodedState);
}
}
'알고리즘 > 다익스트라' 카테고리의 다른 글
| [백준 13549] 숨바꼭질3 / 자바 / 다익스트라 알고리즘 (2) | 2024.09.14 |
|---|---|
| [프로그래머스 LV3] 스킬 체크 / 자바 / 다익스트라 알고리즘 (0) | 2024.07.02 |
| [백준] 최단경로 / 자바 (2) | 2024.05.28 |
| [백준] 파티 / 자바 (0) | 2024.05.27 |




