#문제
레벨: G2
알고리즘: dfs
풀이시간: 1시간
힌트 참조 유무: 유
https://www.acmicpc.net/problem/2250
#문제 풀이
처음에는 이런 생각을 했다.
가장 오른쪽에 있는 노드를 찾은 후 같은 레벨에 있고 가장 왼쪽에 있는 노드를 찾은 것을 이용하여 구한 값과, 가장 왼쪽에 있는 노드를 찾은 후 같은 레벨에 있고 가장 오른쪽에 있는 노드를 찾은 것을 이용하여 구한 값 중 최솟값을 구한다. 그러나 나 너무 지엽적인 방법이기도 하고 깊이와 x값을 성정하는 dfs 하나 가장 오른쪽 노드 찾는 dfs 하난 가장 왼쪽 노드 찾는 dfs 하나 dfs를 총 세 번 돌아야 한다.
위 방법보다 더 좋은 방법을 소개하겠다.
바로 dfs함수 하나에서 레벨과 x좌표와 그 레벨에서 가장 왼쪽에 있는 노드와 가장 오른쪽에 있는 노드를 구하는 것이다.
dfs가 거치는 순서는 x 좌표를 설정하는 것 때문에 맨 아래 왼쪽에서부터 탐색을 한다. 즉, inorder 순서대로 탐색을 한다.
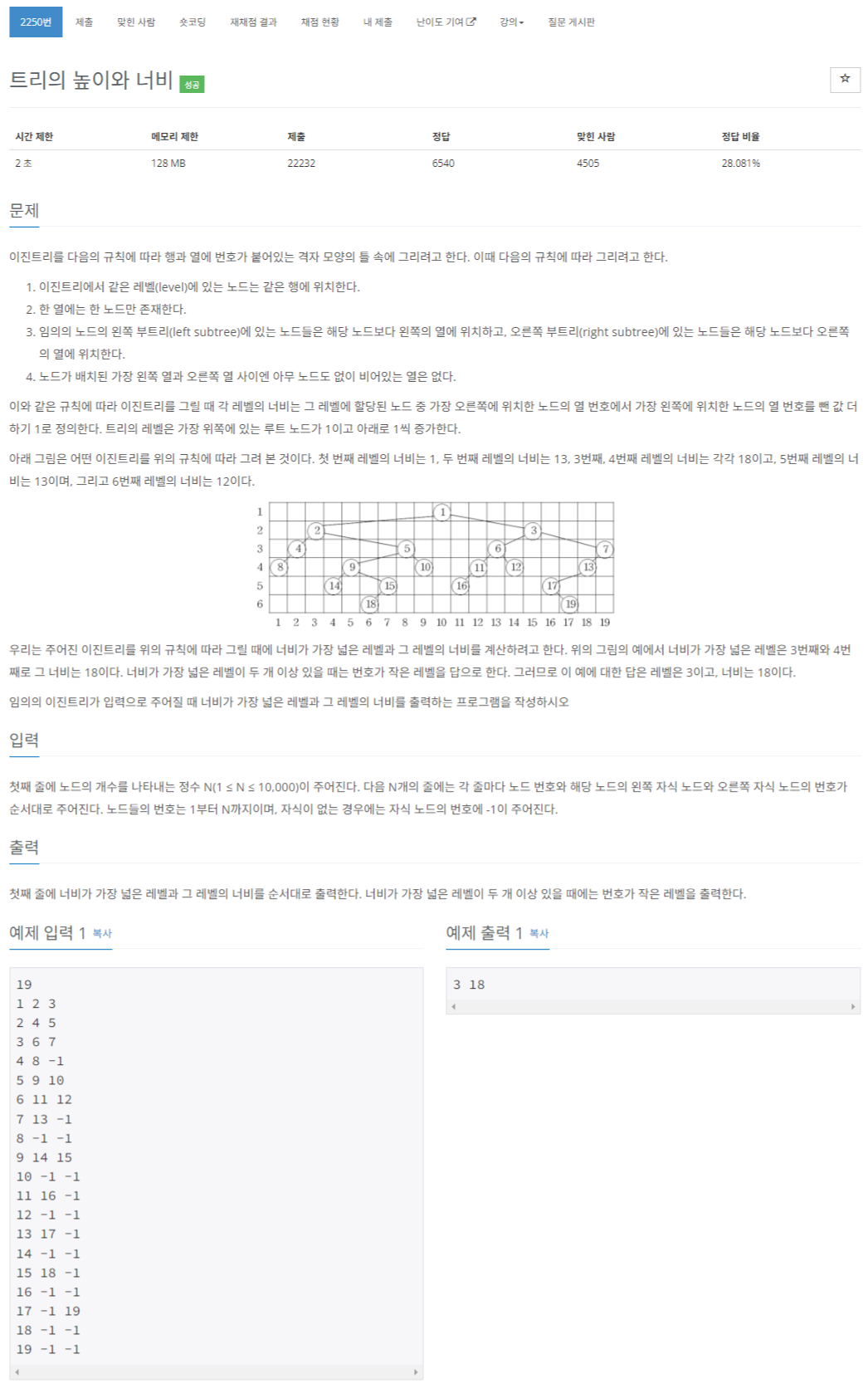
아래 그림으로 예시를 들어보겠다. 괄호 안에 들어가있는 것들은 x좌표를 나타내기도 하지만 탐색 순서(inorder)를 나타내기도 한다.
1(4)
/ \
2(2) 3(6)
/ \ / \
4(1) 5(3) 6(5) 7(7)
괄호 안의 숫자가 각 노드의 x 좌표이다.
레벨 3(가장 아래 레벨)일 때로 예를 들면:
노드 4를 만났을 때: levelMin[3] = levelMax[3] = 1
노드 5를 만났을 때: levelMin[3] = 1, levelMax[3] = 3
노드 6을 만났을 때: levelMin[3] = 1, levelMax[3] = 5
노드 7을 만났을 때: levelMin[3] = 1, levelMax[3] = 7#풀이 코드
import java.util.*;
import java.io.*;
public class Main {
static class Node {
int data;
Node left, right;
Node(int data) {
this.data = data;
}
}
static Node[] nodes;
static int[] levelMin, levelMax;
static int x = 1;
static boolean[] isChild;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
nodes = new Node[N + 1];
levelMin = new int[10001];
levelMax = new int[10001];
isChild = new boolean[N + 1];
for (int i = 1; i <= N; i++) {
nodes[i] = new Node(i);
levelMin[i] = Integer.MAX_VALUE;
}
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
int data = Integer.parseInt(st.nextToken());
int left = Integer.parseInt(st.nextToken());
int right = Integer.parseInt(st.nextToken());
if (left != -1) {
nodes[data].left = nodes[left];
isChild[left] = true;
}
if (right != -1) {
nodes[data].right = nodes[right];
isChild[right] = true;
}
}
int root = findRoot(N);
inOrder(nodes[root], 1);
int maxWidth = 0;
int maxLevel = 0;
for (int i = 1; i <= 10000; i++) {
if (levelMin[i] == Integer.MAX_VALUE) break;
int width = levelMax[i] - levelMin[i] + 1;
if (width > maxWidth) {
maxWidth = width;
maxLevel = i;
}
}
System.out.println(maxLevel + " " + maxWidth);
}
static int findRoot(int N) {
for (int i = 1; i <= N; i++) {
if (!isChild[i]) return i;
}
return 1; // 이 경우는 발생하지 않아야 합니다.
}
static void inOrder(Node node, int level) {
if (node == null) return;
inOrder(node.left, level + 1);
x++;
levelMin[level] = Math.min(levelMin[level], x);
levelMax[level] = Math.max(levelMax[level], x);
inOrder(node.right, level + 1);
}
}
'알고리즘 > DFS' 카테고리의 다른 글
| [백준 16724] 피리 부는 사나이 / 자바 / dfs (0) | 2024.07.31 |
|---|---|
| [백준 1405] 미친 로봇 / 자바 / dfs (0) | 2024.07.30 |
| [백준 10159] 저울 / 자바 / dfs (0) | 2024.07.25 |
| [백준 3548] 가장 가까운 공통 조상 / 자바 / dfs +LCA (0) | 2024.07.25 |
| [백준 17472] 다리 만들기2 / 자바 / dfs + 크루스칼 알고리즘 ** (2) | 2024.07.24 |



