[백준] 2048(Easy) / 자바(feat 브루트 포스, 백트래킹, DFS 차이점)

문제         

레벨: G2
알고리즘: 브루트 포스
풀이시간:  1시간
힌트 참조 유무: 유

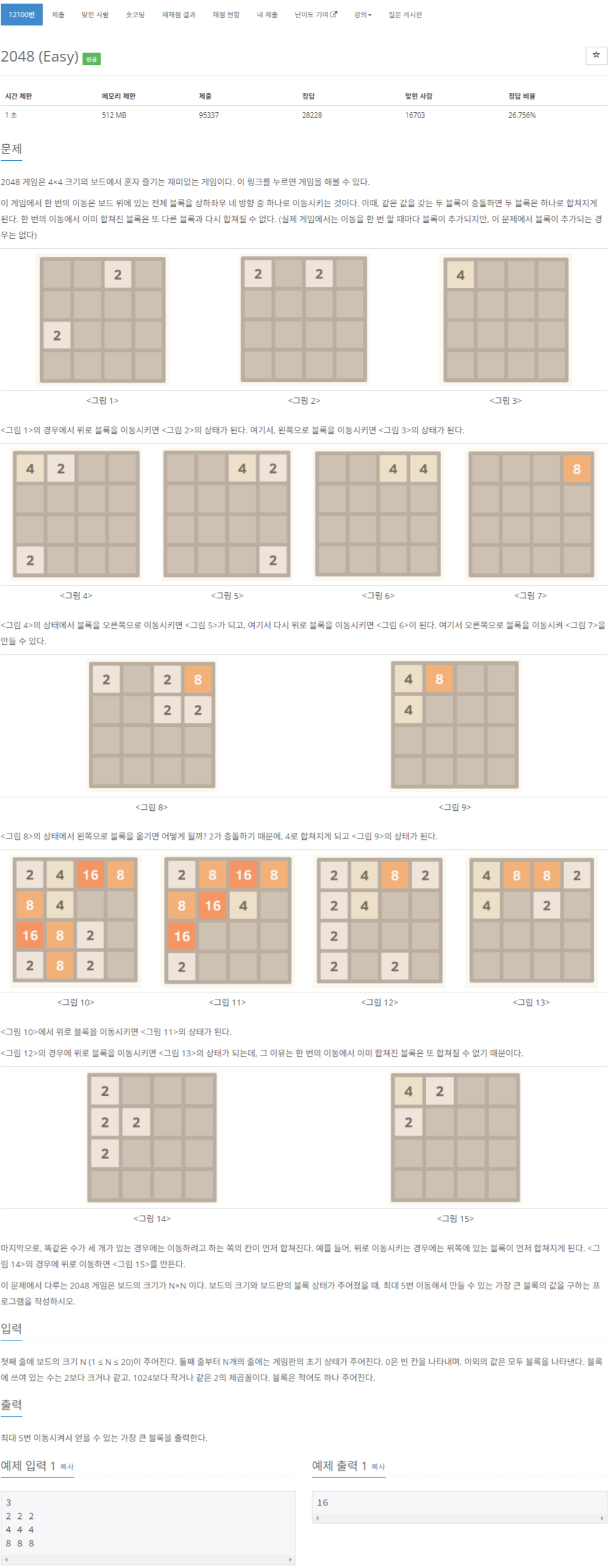
https://www.acmicpc.net/problem/12100

1 번째 시도   

[사고 과정]

• 이 게임의 규칙을 못 찾겠다.
• 최대 N= 20 최대 탐색횟수 5번,  20*20*5 =2,000이므로 완전탐색이 가능할 것 같다.
• 5번의 완전탐색으로 구현 
• 자! 그렇다면 어느 것을 기준으로 탐색해야 할까?
• 각각의 숫자들을 타겟 or 방향
• 각각의 숫자들을 초점에 맞추어 방향을 바꾸어 본다면 다른 숫자들도 영향을 받기 때문에 머리가 너무 아프다
• 당연히 4가지로만 나누어진 방향에 초점을 맞추는 게 맞다!(이번 기회를 통해 어는 것의 초점을 맞추어 탐색할지 중요할 것을 알았다)

 

[구현 할 때 힘든 점]

• 스크롤한 후 배열의 결과를 구현하기가 힘들었다.
• 합칠 수 있는 숫자들을 합친 후 스크롤 방향으로 다 밀어버리려고 생각했는데 구현이 힘들어서 포기했다.
• 새로운 배열을 만들고 차곡 차곡 쌓는 느낌으로 구현했다.
• index와 block으로 합치거나 쌓는 것을 조절했다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    
    static int n, answer, map[][];
    
    public static void main(String[] args) throws Exception {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.parseInt(br.readLine());
        answer = 0;
        map = new int[n][n];
        StringTokenizer stz;
        for(int i = 0; i < n; i++) {
            stz = new StringTokenizer(br.readLine());
            for(int j = 0; j < n; j++)
                map[i][j] = Integer.parseInt(stz.nextToken());
        }

        game(0, map);
        System.out.println(answer);

   
    }
    
    public static void game(int count, int[][] currentMap) {
        if(count == 5) {
            findMax(currentMap);
            return;
        }
        
        for(int i = 0; i < 4; i++) {
            int[][] newMap = move(i, currentMap);
            game(count + 1, newMap);
        }
    }
    
    public static int[][] move(int dir, int[][] currentMap) {
        int[][] newMap = new int[n][n];
        
        switch(dir) {
            // Move up
            case 0:
                for(int i = 0; i < n; i++) {
                    int index = 0;
                    int currentBlock = 0;
                    for(int j = 0; j < n; j++) {
                        if(currentMap[j][i] != 0) {
                            if(currentBlock == currentMap[j][i]) {
                                newMap[index - 1][i] = currentBlock * 2;
                                currentBlock = 0;
                            } else {
                                currentBlock = currentMap[j][i];
                                newMap[index][i] = currentBlock;
                                index++;
                            }
                        }
                    }
                }
                break;
            // Move down
            case 1:
                for(int i = 0; i < n; i++) {
                    int index = n - 1;
                    int currentBlock = 0;
                    for(int j = n - 1; j >= 0; j--) {
                        if(currentMap[j][i] != 0) {
                            if(currentBlock == currentMap[j][i]) {
                                newMap[index + 1][i] = currentBlock * 2;
                                currentBlock = 0;
                            } else {
                                currentBlock = currentMap[j][i];
                                newMap[index][i] = currentBlock;
                                index--;
                            }
                        }
                    }
                }
                break;
            // Move left
            case 2:
                for(int i = 0; i < n; i++) {
                    int index = 0;
                    int currentBlock = 0;
                    for(int j = 0; j < n; j++) {
                        if(currentMap[i][j] != 0) {
                            if(currentBlock == currentMap[i][j]) {
                                newMap[i][index - 1] = currentBlock * 2;
                                currentBlock = 0;
                            } else {
                                currentBlock = currentMap[i][j];
                                newMap[i][index] = currentBlock;
                                index++;
                            }
                        }
                    }
                }
                break;
            // Move right
            case 3:
                for(int i = 0; i < n; i++) {
                    int index = n - 1;
                    int currentBlock = 0;
                    for(int j = n - 1; j >= 0; j--) {
                        if(currentMap[i][j] != 0) {
                            if(currentBlock == currentMap[i][j]) {
                                newMap[i][index + 1] = currentBlock * 2;
                                currentBlock = 0;
                            } else {
                                currentBlock = currentMap[i][j];
                                newMap[i][index] = currentBlock;
                                index--;
                            }
                        }
                    }
                }
                break;
        }
        return newMap;
    }
    
    public static void findMax(int[][] currentMap) {
        for(int i = 0; i < n; i++)
            for(int j = 0; j < n; j++)
                answer = Math.max(answer, currentMap[i][j]);
    }
}

 

 

브루트포스, 백트래킹, DFS 차이

브루트 포스 알고리즘 = 모든 가능한 경우를 전부 해보는 방식의 알고리즘
백트래킹 = 탐색을 진행하고 조건에 맞지 않는 부분을 제외하면서 진행하는 방식의 알고리즘
DFS = 트리를 완전 탐색하는 한가지 방법