[백준] 하노이 탑 이동 순서 / 자바

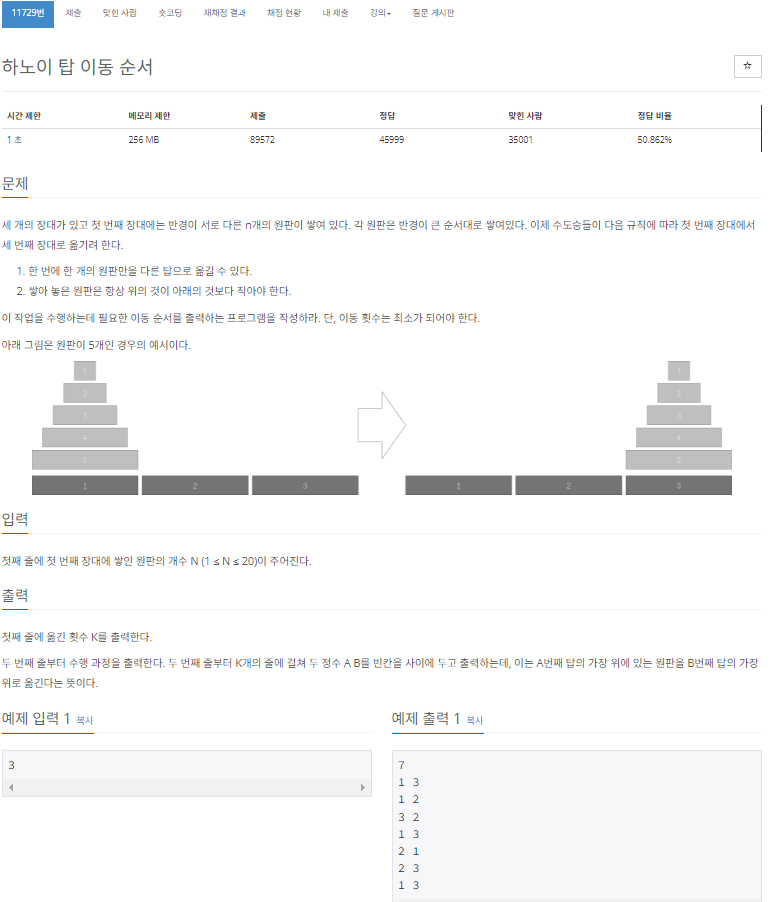
문제         

레벨: G5
알고리즘:  재귀
풀이시간: 1시간
힌트 참조 유무: 유

https://www.acmicpc.net/problem/11729

1 번째 시도   

 

1. 하노이 탑에 기본 원리

가장 큰 원판을 C로 옮기기 위해서는 n-1개의 원판이 A에서 B로 가야한다.

• Hanoi(n) = 2 × Hanoi(n-1) + 1
  • 1은 가장 큰 원판이 C로 간 것
  • 2 x Hanoi(n-1)은 B로 잠깐 옮겨졌다가 최종 목적지인 C로 옮겨진 걸 뜻함

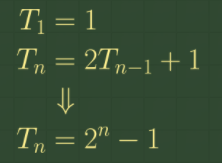
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
 
	public static StringBuilder sb = new StringBuilder();
 
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
 
		int N = Integer.parseInt(br.readLine());
 
		sb.append((int) (Math.pow(2, N) - 1)).append('\n');
 
		Hanoi(N, 1, 2, 3);
		System.out.println(sb);
 
	}
 
	/*
		N : 원판의 개수 
		start : 출발지 
		mid : 옮기기 위해 이동해야 장소 
		to : 목적지
	 */
 
	public static void Hanoi(int N, int start, int mid, int to) {
		// 이동할 원반의 수가 1개라면?
		if (N == 1) {
			sb.append(start + " " + to + "\n");
			return;
		}
 
		// A -> C로 옮긴다고 가정할 떄,
		// STEP 1 : N-1개를 A에서 B로 이동 (= start 지점의 N-1개의 원판을 mid 지점으로 옮긴다.)
		Hanoi(N - 1, start, to, mid);
    
		// STEP 2 : 1개를 A에서 C로 이동 (= start 지점의 N번째 원판을 to지점으로 옮긴다.)
		sb.append(start + " " + to + "\n");
    
		// STEP 3 : N-1개를 B에서 C로 이동 (= mid 지점의 N-1개의 원판을 to 지점으로 옮긴다.)
		Hanoi(N - 1, mid, start, to);
	}
}